PyTorch 是一个开源的 Python 机器学习库，基于 Torch，底层是由 C++ 实现，可以加速研究成果产业化。

我们的项目本次使用 PyTorch 来进行开发，在 2021 年初的时候我曾在 B 站简单地学习了吴恩达教授的机器学习课程[1]，对整个机器学习的原理有了初步了了解，在他的视频中有具体对函数的原理及其推导过程，但是他的教程是基于 TensorFlow 的，和 PyTorch 不太一样，所以我们后面还学习了李宏毅教授的机器学习理论课[2]，两位大佬将背后的细节讲的非常深入。除此之外，我们还学习了莫凡 Python 的 PyTorch 课程[3]。

本文将分为六个部分，PyTorch 常用语法，激活函数，数据批标准化，回归神经网络搭建，超参数调节，训练可视化。

拟合（回归）网络适合参数的预测，比如在房屋销售价格预测中，输入一组 <房屋面积,房间数,地区,…> 等特征，神经网络需要预测并输出<房价>。

一、PyTorch 常用语法

为了完成上述例子的预测，要先了解一下 PyTorch 的基本语法

torch.Tensor 包含单一数据类型的元素的多维矩阵（张量）。我们可以用 Tensor([房间面积,房间数,地区,…]) 来作为特征

torch.nn.Module 作为模型基类，定义一个 class Net(orch.nn.Module) 作为我们的神经网络模型

model = Net() 初始化我们的模型

torch.save(model.state_dict(), 'model.pl') 将训练好的模型保存至硬盘

model.load_state_dict(torch.load('model.pl')) 将模型加载入内存

model.eval() 用于在测试前固定训练好的各种参数

固定参数后使用 model(torch.Tensor([房间面积,房间数,地区,...])) 即可获得预测张量

Tensor.item() 用于将一个1×1的张量转换为对应类型的数据

二、激活函数（Activation Function）

我们先来看看深度学习中常见的几种激活函数的函数图像

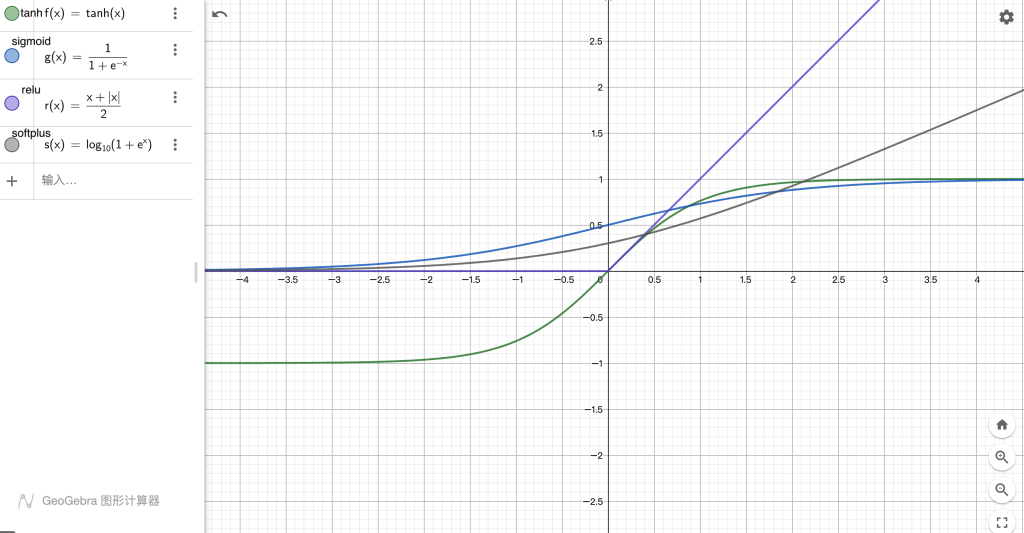
PyTorch 入门与回归网络搭建的研究-Jacky's Blog

对于 relu 函数，x < 0 的部分都是 0，x > 0 的部分为 x。对于 sigmoid 函数，x 在 [-4, 4] 之间变化时 sigmoid(x) 明显，超出范围处在函数的饱和阶段。对于 tanh 函数，x 在 [-2, 2] 之间变化时 tanh(x) 变化明显，超出范围处在函数的饱和阶段。对于 softplus 函数，当 x 处在 (-∞, -3] 时几乎无变化，当 x > -3 时，softplus(x) 变化明显。

当 Tensor 传入激活函数时，执行的是广播操作，即对矩阵中的每行每列的元素都进行 f(x) 运算。

三、数据批标准化（Batch Normalization, BN）

为什么要进行批标准化？

数据批标准化有利于机器找到其中的规律

在上一部分的激活函数的图像分析中，我们发现，若使用 relu/softplus 则负值的激活函数值为 0，或数据过大时，tanh，sigmoid 的值处于饱和区域，使得神经元对该数据变得不敏感，最终的拟合结果与实际的结果相差甚远。因此，我们需要将数据批标准化，使每一层输出的数据的均值为0，方差为1。

Batch Normalization，中 Batch 是批数据，将数据分成小批小批进行随机梯度下降（Stochastic Gradient Descent），而且在每批数据在进行向前传递（Forward Propagation）时，对每一层都进行 Normalization 处理[3]。批标准化不需要在 Excel 中进行处理，PyTorch 提供了批标准化的方法，在搭建神经网络时使用即可，在下一个部分中将会介绍。

四 、回归神经网络搭建

以下是网络搭建的基本类，我们需要构造一个神经网络的模型类，继承 torch.nn.Module 类，实现 __init__ 函数和 forward 函数。

class Net(torch.nn.Module):
    def __init__(self):
        pass
        

    def forward(self, x):
        pass

这里参考莫凡 Python 的搭建方法，给出搭建的模板，根据数据的情况来修改超参数

import torch

# Hyper parameters 超参数
N_INPUT = 4 # 输入维度
N_HIDDEN_LAYER = 20 # 隐藏层的数量
N_HIDDEN = 130 # 每个隐藏层包含的神经元个数
N_OUTPUT = 3 # 输出维度
ACTIVATION = torch.tanh # 激活函数
EPOCH = 1000000 # 训练次数
LR = 0.000001 # 学习率
B_INIT = -0.2  # use a bad bias constant initializer


class Net(torch.nn.Module):
    def __init__(self):
        # 初始网络的内部结构
        super(Net, self).__init__()
        self.fcs = []
        self.bns = []
        # 输入批标准化
        self.bn_input = torch.nn.BatchNorm1d(N_INPUT, momentum=0.5)
        for i in range(0, N_HIDDEN_LAYER):
            input_size = N_INPUT if i == 0 else N_HIDDEN
            fc = torch.nn.Linear(input_size, N_HIDDEN)
            setattr(self, 'fc%i' % i, fc)
            # 参数初始化
            self._set_init(fc)
            self.fcs.append(fc)
            # 每层神经元的输出后加入批标准化层
            bn = torch.nn.BatchNorm1d(N_HIDDEN, momentum=0.5)
            setattr(self, 'bn%i' % i, bn)
            self.bns.append(bn)
        # 输出层
        self.predict = torch.nn.Linear(N_HIDDEN, N_OUTPUT)
        # 参数初始化
        self._set_init(self.predict)

    @staticmethod
    def _set_init(layer):
        torch.nn.init.normal_(layer.weight, mean=0, std=.1)
        torch.nn.init.constant_(layer.bias, B_INIT)

    def forward(self, x):
        # 一次正向行走过程
        x = self.bn_input(x)

        for i in range(N_HIDDEN_LAYER):
            x = self.fcs[i](x)
            x = self.bns[i](x)
            x = ACTIVATION(x)
        # output
        x = self.predict(x)
        return x

五、超参数调节

首先简单说一下欠拟合和过拟合，欠拟合就是训练集的数据丢给网络预测之后的结果与原来的结果相差很大，即训练集的拟合效果差，而过拟合则是训练集数据的预测（拟合）结果与原来的结果相差非常小，几乎完美，但是输入测试集去测试时拟合效果又非常差，一般出现于训练集数据较少的情况。

当我们顺利完成拟合之后，又花费了很大时间在超参数调节上。调节超参数可以得到更好的训练效果/效率，对于隐藏层的数量，我们在自己测试的时候也发现，增加层数理论上拟合函数的能力更强，拟合效果应该更强，但是层数越深，训练的难度就越大，需要耗费大量的时间，且模型难以收敛，过大的层数效果并不理想。因此在选择层数的时候可以遵循以下规则：

  • 没有隐藏层：仅能够表示线性可分函数或决策
  • 隐藏层数=1：可以拟合任何“包含从一个有限空间到另一个有限空间的连续映射”的函数
  • 隐藏层数=2：搭配适当的激活函数可以表示任意精度的任意决策边界，并且可以拟合任何精度的任何平滑映射
  • 隐藏层数>2：多出来的隐藏层可以学习复杂的描述（某种自动特征工程）

经过大量调整，最后将找到了相对合适的一组隐藏层的个数和每层神经元的数量，在当前较少数据的情况下得到了良好的拟合效果。

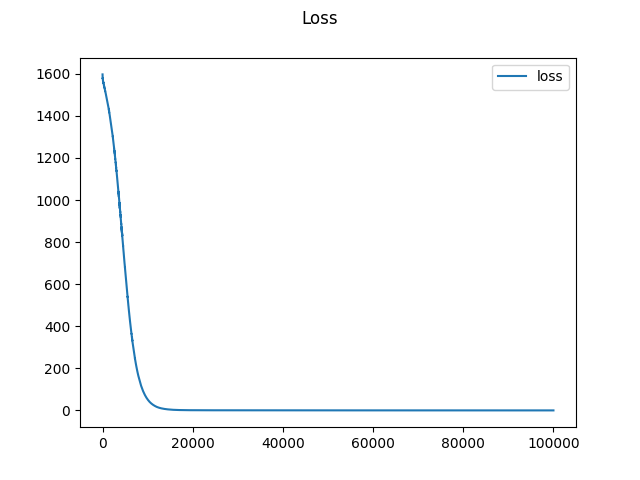
接下来讲一下训练次数和学习率，更小的学习率可以获得更好的学习效果，但也需要更大的训练次数，但具体需要训练多少次，可以通过 loss 值来判断，这里我们可以通过绘图来得到。

PyTorch 入门与回归网络搭建的研究-Jacky's Blog

六、训练可视化

这都是一些简单的程序设计，炼丹的时候往往需要耗费大量的时间和算力，不做适当的输出也不知道计算机干到什么情况了。因此我使用 rich.progress 来显示训练的进度，使用 matplotlib.plot 来绘图，如 loss 值以及测试时的拟合效果。

训练进度条

from rich.progress import track

for i in track(range(EPOCH)):
    prediction = net(x).to(device)
    loss = loss_func(prediction, y).to(device)
    
    optimizer.zero_grad()
    loss.backward()
    optimizer.step()

使用效果

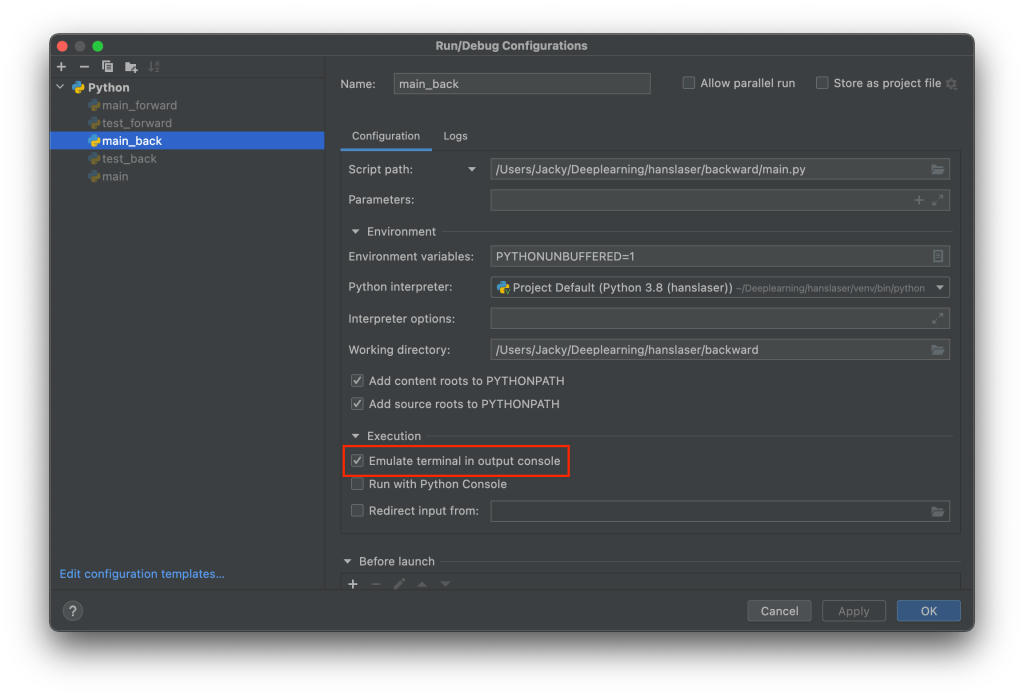
PyTorch 入门与回归网络搭建的研究-Jacky's Blog
rich.progress 进度条

对于 PyCharm 来说，使用 Run 运行时可能不显示进度条，但是在终端里跑可以显示。对于这个问题，可以在运行配置中启用 Emulate terminal in output console

PyTorch 入门与回归网络搭建的研究-Jacky's Blog

绘制 loss 与 EPOCH 的图

loss_list = []
x_list = []
for i in track(range(20000)):
    prediction = net(x).to(device)
    loss = loss_func(prediction, y).to(device)
    loss_list.append(loss.item())
    optimizer.zero_grad()
    loss.backward()
    optimizer.step()
    x_list.append(i)

# 绘图
fig, ax = plt.subplots()

ax.plot(x_list, loss_list, label='loss')
ax.legend()

fig.suptitle('Loss')
plt.show()

绘图效果

PyTorch 入门与回归网络搭建的研究-Jacky's Blog
loss 与 EPOCH 关系

引用

[1] [双语字幕]吴恩达深度学习deeplearning.ai, https://www.bilibili.com/video/BV1FT4y1E74V
[2] (强推)李宏毅2021春机器学习课程， https://www.bilibili.com/video/BV1Wv411h7kN
[3] PyTorch | 莫凡 Python，https://mofanpy.com/tutorials/machine-learning/torch/
[4] 如何确定神经网络的层数和隐藏层神经元数量, https://zhuanlan.zhihu.com/p/100419971

文章最后修订于 2022年3月7日